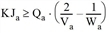Da die Analyse in einem dynamischen Kontext ausgeführt wird, sind die Modellvariablen Ganglinien, die hier als stückweise konstante Funktionen der zeitlichen Variable t dargestellt werden.
Nutzerfahrten im Streckennetz werden mit einem gerichteten Graph G = (N, A) modelliert, wobei N die Menge der Knoten und A⊆N ´ N die Menge der Kanten ist. Jede Strecke, jeder Abbieger und jede Anbindung im Visum-Netz entspricht einer Kante. Jeder Visum-Netzknoten und Bezirk entspricht einem Knoten von G.
Jede Kante a wird definiert durch ihren Anfangsknoten TL(a) und ihren Endknoten HD(a).
Also ergibt sich a = (TL(a), HD(a)).
Beispiel
Im Fall einer Kante a, die eine Strecke im Visum-Netz darstellt, würde TL(a) deren Von-Knoten und HD(a) deren Nach-Knoten entsprechen. Ausgehende und eingehende Kanten des Knoten x∈N sind angegeben als FS(x) ={a∈A: x = TL(a)} oder BS(y) = {a∈A: y = HD(a)}. Die Bezirke bilden eine Teilmenge Z ⊆ N der Knoten.
Nutzer, die von einem Knoten o∈N zu einem Knoten d∈Z fahren, ziehen die Menge Kod aller Wege in Betracht, die o und d auf G verbinden. Im Vordergrund steht das n:1 Kurzwegproblem von jedem Knoten o∈N zu einem gegebenen Ziel d∈Z. Es wird davon ausgegangen, dass Graph G stark zusammenhängend ist, sodass Kxd mit x∈N ≠ d∈Z nicht leer ist.
Folgende festgelegte Schreibweise beschreibt die Wegetopologie:
A(k) = Folge von Kanten, die den Weg k∈Kod von o∈N nach d∈Z festlegt
Für die Netzbelastungen werden folgende Schreibweisen genutzt:
|
Dod(τ) |
Nachfrage von Fahrzeugen, die sich von Quelle o∈N zu Ziel d∈Z bewegen und zum Zeitpunkt τ abfahren |
|
fa(τ) |
Fluss von Fahrzeugen, die zum Zeitpunkt τ Kante a∈A befahren |
|
Fa(τ) |
kumulierter Fluss von Fahrzeugen, die zum Zeitpunkt τ Kante a∈A befahren |
|
ua(τ) |
Abfluss von Kante a∈A zum Zeitpunkt τ |
Definitionsgemäß gilt Folgendes:
Für die Netzleistungen werden Reisezeiten durch Zu- und Abflussfunktionen dargestellt und folgende Schreibweisen genutzt:
|
ca(τ) |
Kosten, um Kante a∈A zu befahren für Fahrzeuge, die zum Zeitpunkt τ auffahren |
|
ta(τ) |
Abflusszeit von Kante a∈A für Fahrzeuge, die zum Zeitpunkt τ auffahren |
|
fa-1(τ) |
Zuflusszeit von Kante a∈A für Fahrzeuge, die die Kante zum Zeitpunkt τ verlassen |
|
Ck(τ) |
Kosten von Weg k∈Kod von o∈N nach d∈Z für Fahrzeuge, die Knoten o zum Zeitpunkt τ verlassen |
|
Tk(τ) |
Abflusszeit von Weg k∈Kod von o∈N nach d∈Z für Fahrzeuge, die o zum Zeitpunkt τ verlassen |
Da es zeitlich veränderliche Kosten gibt, kann es vorteilhaft sein, an Knoten zu warten, um eine bestimmte Kante zu einem späteren Zeitpunkt zu befahren. Im Folgenden wird davon ausgegangen, dass Fahrzeuge nicht an Knoten warten dürfen, stattdessen können aber Wege mit Zyklen vorteilhaft erscheinen. Die dynamischen Kurzwege enthalten jedoch höchstens eine endliche Anzahl von Zyklen.
Da das Warten an Knoten nicht zugelassen ist, ist die Reisezeit Tk(τ) eines Weges die Summe der Reisezeiten seiner Kanten A(k), wobei jeweils die zu dem Zeitpunkt gültige Kantenreisezeit verwendet wird, zu dem die Fahrzeuge die Kante erreichen. Gleiches gilt für die Berechnung der Wegekosten Ck(τ) als Summe der Kosten der Kanten A(k). Die Abflusszeit beziehungsweise die Kosten von Weg k können dann über folgende rekursive Gleichungen ermittelt werden:
Dabei ist a = (o, x)∈A die erste Kante von k und h∈Kxd der Rest des Weges k (Abbildung 118).
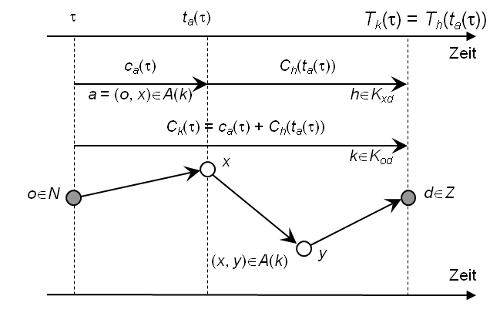
Abbildung 118: Rekursive Gleichungen der Wegabflusszeit, -zuflusszeit und Kosten
Die strikte FIFO-Regel gilt, wenn folgende Eigenschaft für jede Kante a∈A erfüllt wird:
Die durch [30] ausgedrückte Monotonie garantiert, dass die Ganglinien der Kantenabflusszeit umkehrbar sind. Die FIFO-Regel gilt ferner auch für die Zuflusszeiten.
Jede Kante a∈A besteht aus einer homogenen Verbindung mit zwei Engpässen, die am Anfang und am Ende liegen. Die Belastungen entlang der Kante werden auf der Basis der Vereinfachten Theorie kinematischer Wellen (STKW) und des Fundamentaldiagramms in Abbildung 119 ermittelt und geben die Fahrzeugbelastung qa(x,τ) auf einem bestimmten Abschnitt x der Kante zu einem bestimmten Zeitpunkt t als Funktion der Fahrzeugdichte ka(x,τ) auf demselben Abschnitt zum selben Zeitpunkt wieder.
Die Kante ist dann folgendermaßen gekennzeichnet:
|
La |
Länge der Kante a |
|
Qa |
Kapazität des ersten Engpasses und der mit Kante a assoziierten homogenen Verbindung, Eingangskapazität genannt |
|
Sa |
Kapazität des letzten mit Kante a assoziierten Engpasses, welche den durchschnittlichen Effekt der Reduzierung der Kapazität an Knotenpunkten simuliert (zum Beispiel durch vorhandene LSA), Ausgangskapazität genannt Sa ≤ Qa; |
|
Va |
maximale auf Kante a erlaubte Geschwindigkeit, in Visum üblicherweise v0 genannt |
|
KJa |
maximale Dichte auf Kante a, maximale Staudichte genannt |
|
Wa |
Fortpflanzungsgeschwindigkeit der überkritischen Belastungen auf Kante a, Stauwellengeschwindigkeit genannt |
Vor diesem Hintergrund ist die Eingangskapazität gleich der physikalischen Kapazität auf der freien Strecke, wogegen die Ausgangskapazität gleich der auf Lichtsignalanlagen oder Vorfahrtsregeln beruhenden Engpasskapazität am stromabwärtigen Knotenpunkt ist. Zielanbindungen (x, d)∈A: x∈N \ Z, d∈Z sind Kanten mit unbegrenzter Eingangskapazität, Quellanbindungen (o, y)∈A: o∈Z, y∈N \ Z sind Kanten mit unbegrenzter Ausgangskapazität. Abbieger sind hingegen Kanten der Länge null, deren Eingangskapazitäten und Ausgangskapazitäten gleich sind.
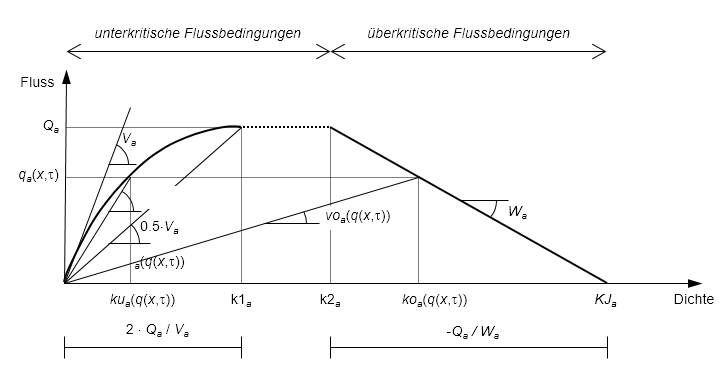
Abbildung 119: Das parabolische Fundamentaldiagramm, das die Relation zwischen Verkehrsstärke, Geschwindigkeit und Dichte entlang einer bestimmten Kante wiedergibt.
In Abbildung 119 muss k2a ≥ k1a gelten, was folgende Ungleichung unter den obigen Parametern voraussetzt:
Auf der Basis des Fundamentaldiagramms können zwei Flusszustände unterschieden werden.
- Unterkritische Flussbedingungen, das heißt nicht überlasteter oder leicht überlasteter Verkehr. Wenn unter diesen Bedingungen die Fahrzeugdichte zunimmt, nimmt auch die Verkehrsstärke zu.
- Überkritische Flussbedingungen, das heißt stark überlasteter Verkehr. Staus und „Stop and go”-Phänomene kommen vor. Nimmt unter diesen Bedingungen die Fahrzeugdichte weiter zu, so nimmt die Verkehrsstärke ab.
Dann drücken koa(q) und voa(q) die Dichte und die Geschwindigkeit als Funktionen der Belastung unter überkritischen Belastungszuständen aus, während kua(q) und vua(q) der Dichte und Geschwindigkeit als Funktionen der Belastung unter unterkritischen Belastungszuständen entsprechen.
Werden Kanten mit niedrigen Geschwindigkeitsbegrenzungen modelliert, die innerstädtische Strecken darstellen, kann unter unterkritischen Belastungsbedingungen von einer konstanten Fahrzeuggeschwindigkeit ausgegangen werden, die der Geschwindigkeitsbegrenzung entspricht, bis die Kapazität erreicht ist. In diesem Fall kann das in Abbildung 120 dargestellte einfachere trapezförmige Fundamentaldiagramm angewandt werden, wobei folgende Gleichung erfüllt sein muss, damit k2a ≥ k1a gilt:
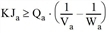
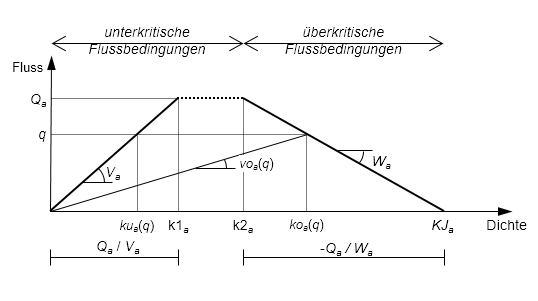
Abbildung 120: Das für innerstädtische Strecken empfohlene trapezförmige Fundamentaldiagramm
Um die vorgeschlagenen Modelle zu implementieren, wird die Analyseperiode [0, Q] in n Zeitintervalle unterteilt, gekennzeichnet durch die Folge der Zeitpunkte τ= {τ0, … , τi, … , τn},wobei τ0 = 0, τi < τj für alle 0 ≤ i < j ≤ n, und τn= Q. Für Berechnungszwecke wird zudem ein zusätzlicher Zeitpunkt τn+1= ∞ eingeführt.
Nachfolgend wird die Ganglinie g(τ) jeder Variable entweder über eine stückweise lineare oder eine stückweise konstante Funktion angenähert, definiert durch die Werte gi = g(τi) zu jedem Zeitpunkt τi∈τ. So kann jede Ganglinie g(τ) über den Vektor g = (g0, … , gi, … , gn) numerisch dargestellt werden.
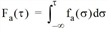
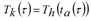
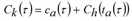
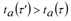 , für alle
, für alle 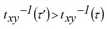 , für alle
, für alle